LEMO

Curvas características de resistores

E1) Para identificar um certo resistor, um grupo de estudantes obteve os seguintes resultados:

V (V)	5,0	10,0	15,0	20,0	25,0
I (mA)	0,103	1,58	8,07	25,63	62,50

a) Qual era o tipo de Resistor? Justifique.

(   )Filamento incandescente          (   ) VDR          (   ) Ôhmico          (   ) PTC          (   ) Outro

b) Construa uma gráfico adequado e identifique os parâmetros deste resistor (se isto for possível).

E2) Medindo-se a diferença de potencial (em Volts) e a intensidade de corrente elétrica (em mA) sobre um varistor (VDR) obteve-se o gráfico (di-log) abaixo. A partir do gráfico obtido, determine:

a) A diferença de potencial, em volts, quando o varistor estiver sendo percorrido por uma corrente de 0,47 mA. 
b) A resistência elétrica do varistor, em kΩ, quando o mesmo estiver submetido a uma diferença de potencial de 7,8 V.

E3) Um grupo de alunos obteve a tabela abaixo, na temperatura T₁ = 22,0 ºC, com a finalidade de construir a curva característica de um termistor:

V (volts)	8,00	28,0	40,0	60,0	100	120
i (mA)	4,0	14	20	24	18	12

a) A partir dos dados da tabela, nota-se um comportamento ôhmico até qual tensão? Qual o valor da resistência?

b) Se aplicarmos uma tensão de 15,0 V no termistor, qual o valor da corrente que circulará?

c) Admita agora que o termistor tenha sido aquecido até uma temperatura T₂ = 42,0 ºC , mantendo comportamento ôhmico para baixas tensões e atingindo uma corrente i = 10 mA para uma tensão aplicada V₂ = 26,0 V. Comparativamente, à temperatura T₁ = 22,0 ºC , esta corrente era atingida quando aplicava-se uma tensão V₁  = 20,0 V. A partir disso, determine os valores numéricos das resistências elétricas nas temperaturas mencionadas (atenção às unidades).

d) Uma dependência linear da resistência com relação à temperatura pode ser expressa por R₂=R1+ α\Δ T. Supondo, que nosso termistor obedece a esta relação linear, calcule seu coeficiente de temperatura (α).

e) De acordo com o sinal de α encontrado no item anterior, classifique o termistor: trata-se de um PTC ou de um NTC?

Medidas de resistência com a Ponte de Wheatstone

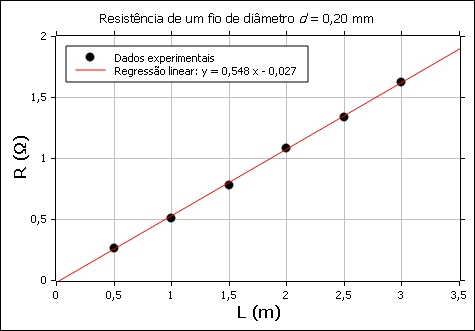
E4) O gráfico abaixo foi obtido medindo-se a resistência R de fios de diferentes comprimentos l, com mesmo diâmetro e feitos do mesmo material ôhmico. Determine a resistividade deste material sabendo que o diâmetro dos fios era d = 0,20 mm.

E5) Ao medir as resistências de um fio de uma certa liga metálica, com um comprimento fixo de 0,2500 metros, utilizando-se uma “Ponte de Wheatstone” na condição de equilíbrio, obteve-se a seguinte tabela:

(a/b)	2,7273	4,0910	6,8182	8,1818
A (10-8 m2)	5,0000	3,333	2,000	1,6666

Sabendo-se que, nessas medidas, R_S era fixo e igual a 11,00 Ω, construa um gráfico adequado e, a partir disso, determine:

a) A resistividade do fio em Ω.m .

b) O valor numérico, em Ω, da resistência do fio, se o comprimento do mesmo for aumentado para 128,15 m e considerando uma área de secção transversal constante e igual a 25,317 x 10^-8 m².

c) Se o resistor do item anterior for associado, em paralelo, com um resistor de 2,7290 ohms e outro de 146,34 ohms, qual o valor da resistência equivalente, em Ω, assim constituída?

E6) Uma ponte de Wheatstone foi equilibrada utilizando-se uma resistência padrão R_S = 30,0 Ω e com o cursor da régua potenciométrica indicando uma razão a/b = 1,90, para um fio condutor de comprimento total igual a 2,50 m. Sabendo-se que o diâmetro, suposto circular, do fio é de 0,030 mm, utilizando a resistividade do metal que constitui este condutor, e com o auxílio da tabela abaixo, identifique o fio, mostrando claramente todos os cálculos efetuados para a determinação de sua resistividade:

Condutor	Al	Fe	W	Ag
r (x10-8 Ω .m):	2,750	9,680	5,250	1,620

Leis de Kirchhoff em circuitos de corrente contínua

E7) Ao fazer a experiência das Medidas em Circuitos de Corrente Contínua, na segunda montagem experimental (o circuito “B”, como é mostrado na imagem abaixo), você utilizou uma fonte estabilizada de tensão contínua, um reostato (resistor variável), uma chave liga-desliga, fios de ligações, um amperímetro, um voltímetro e um resistor de proteção. Suponha que, tal como feito no Laboratório de Eletricidade, tenham sido obtidos os valores a seguir tabelados para quatro diferentes posições do reostato e, com a chave abaixada, registrando-se os seguintes valores de i, em mA, e V, em volts:

V (volts):	3,080	2,300	1,440	0,5500
i (mA):	25,00	200,0	400,0	600,0

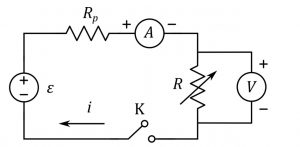 Montagem da segunda parte.

Admitindo que o valor numérico do resistor de proteção R_P é igual a 1,980 Ω então, a partir de um gráfico convenientemente linearizado, determine:

a) A tensão na fonte: ▢ V; e a resistência interna do amperímetro: ▢ Ω.

b) A intensidade da corrente elétrica máxima (corrente de curto-circuito), em mA, capaz de circular nesse circuito.

c) O valor da potência elétrica dissipada no reostato, em watts, quando o circuito é percorrido por uma intensidade de corrente de 325,00 mA.

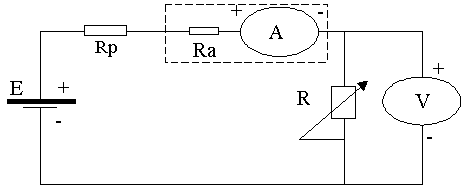
E8) Uma fonte de tensão de 6,0 V de f.e.m. e resistência interna considerada como nula, foi conectada a um circuito idêntico ao utilizado na parte “B” da experiência realizada no laboratório. Quando a diferença de potencial nas extremidades do resistor variável R era 3,21 V, circulava uma corrente, em A, igual a i₁. Em uma outra situação, variando R, para uma intensidade de corrente igual a 0,24 A, mediu-se uma diferença de potencial V₂, em Volts, entre as extremidades de R. Considerando a resistência interna do amperímetro e o resistor de proteção como tendo 2,30 ohms e 13,20 ohms respectivamente, determine: 

a) A corrente elétrica i₁, em A, e a diferença de potencial V₂, em volts, nas situações acima descritas. 
b) O erro relativo percentual das grandezas calculadas no item anterior, sabendo-se que os valores teóricos de ambas são respectivamente iguais a 0,20A e 2,26V.

E9) Com base nos dados abaixo:

a) determine a resistência interna da bateria.

	V (V)	i (A)
Bateria em aberto	11,70	– x –
Bateria no circuito	11,50	0,875

E10) Durante o processo do carregamento de um capacitor de 48 mF, um grupo de alunos utilizou uma fonte de tensão de força eletromotriz constante e igual a 32,00 volts. Obteve-se para os valores das tensões medidas no resistor em função do tempo a seguinte tabela: Carga e descarga de um capacitor (Circuito RC)

Vr (volts)	18,00	8,2000	3,200	0,6900
t(s)	15,0	35,0	60,0	100,0

A partir de um gráfico, confeccionado em papel mono-log, determine:
a) O valor em kW, da resistência utilizada neste circuito RC série.
b) Qual o tempo, em segundos, necessário para o capacitor alcançar 38,75% da força eletromotriz da fonte utilizada?

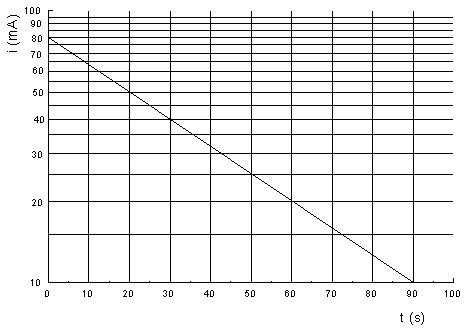
E11) O gráfico da corrente, em micro-ampères, em função do tempo, em segundos, mostrado em seguida, foi obtido durante o processo de carregamento de um capacitor. Nas medidas foi utilizado um resistor de 306 W.  A partir da constante de tempo capacitiva experimental, determine: 
        a) A capacitância, em mF, e a tensão utilizada na fonte.
        b) O tempo necessário para que a tensão, no capacitor, seja 37% da tensão utilizada na fonte.

E12)  Para um Circuito RC em processo de carga foram obtidos os seguintes resultados:

VC (V)	49,2	82,7	105,0	130,1	135,9
Vr (V)	100,5	67,1	44,8	19,7	13,8
t (s)	20	40	60	100	120

Sabendo-se que o resistor tinha uma resistência de 2,5 MΩ, determine, através do gráfico que julgar mais adequado:

a) A constante de tempo do circuito;
b) A tensão inicial aplicada;
c) A carga no capacitor, após 70 s de sua ligação;
d) A corrente no circuito, após 50 s de sua ligação.

Circuito RLC

E13) Um circuito RLC em série, alimentado por uma corrente alternada, apresentou os seguintes resultados:

VR = 4,1 V

VC = 9,7 V

VL = 6,8 V

i = 0,15 A

Sabendo-se que a freqüência utilizada foi de 500 Hz, determine:

a) Os valores de R, L e C utilizados;
b) A frequência teórica de ressonância;
c) A tensão da fonte;
d) A tensão no indutor e no capacitor, em ressonância e na ausência do resistor R, com tensão na fonte V = 2,0 V e corrente máxima de 0,45 A.

E14) As seguintes medidas foram obtidas num circuito RLC série:

I (mA)	VR (V)	VC (V)	VL (V)
50,00	12,19	10,23	4,840

A frequência do gerador estava regulada em 1000,0 Hz, na amplitude máxima e a tensão total, medida nos terminais do gerador, era 13,42 V. A partir disso, determine:

a) A frequência teórica de ressonância, em Hz, para este circuito.
b) Através dos cálculos apropriados, justifique porque este circuito não é indutivo.

E15) Um circuito RLC série foi montado e foi feita uma série de medidas de corrente para a determinação experimental da frequência de ressonância do sistema. Considere que a resistência R do circuito é composta exclusivamente da resistência interna do amperímetro e da resistência ôhmica da bobina, a qual vale 20,0 Ω. Sabendo que a tabela abaixo foi obtida para uma tensão na fonte igual a 0,75 V e que uma das frequências presentes na tabela é a frequência de ressonância, determine a resistência interna do amperímetro em ohms.

i (mA)	5,3	10,0	12,2	18,1	22,0	25,3	30,5	24,5	22,7	16,6	11,8	4,0
f (Hz)	1020	1280	1340	1450	1500	1540	1640	1700	1760	1860	2000	3000